28 мая 2015

Леонард Эйлер (1707-1783) - известный швейцарский и российский математик, член Петербургской академии наук, бо́льшую часть жизни прожил в России. Наиболее известным в математическом анализе, статистике, информатике и логике считается круг Эйлера (диаграмма Эйлера-Венна), используемый для обозначения объема понятий и множеств элементов.

Джон Венн (1834-1923) - английский философ и логик, соавтор диаграммы Эйлера-Венна.

Совместимые и несовместимые понятия

Под понятием в логике подразумевается форма мышления, отражающая существенные признаки класса однородных предметов. Они обозначаются одним либо группой слов: «карта мира», «доминантовый квинтсептаккорд», «понедельник» и др.

В случае когда элементы объема одного понятия полностью или частично принадлежат объему другого, говорят о совместимых понятиях. Если же ни один элемент объема определенного понятия не принадлежит к объему другого, мы имеем место с несовместимыми понятиями.

В свою очередь, каждый из видов понятий имеет собственный набор возможных отношений. Для совместимых понятий это следующие:

• тождество (равнозначность) объемов;
• пересечение (частичное совпадение) объемов;
• подчинение (субординация).

Для несовместимых:

• соподчинение (координация);
• противоположность (контрарность);
• противоречие (контрадикторность).

Схематически отношения между понятиями в логике принято обозначать при помощи кругов Эйлера-Венна.

Отношения равнозначности

В данном случае понятия подразумевают один и тот же предмет. Соответственно, объемы данных понятий полностью совпадают. Например:

А - Зигмунд Фрейд;

В - основоположник психоанализа.

А - квадрат;

В - равносторонний прямоугольник;

С - равноугольный ромб.

Для обозначения используются полностью совпадающие круги Эйлера.

Пересечение (частичное совпадение)

А - педагог;

В - меломан.

Как видно из данного примера, объемы понятий частично совпадают: определенная группа педагогов может оказаться меломанами, и наоборот - среди меломанов могут быть представители педагогической профессии. Аналогичное отношение будет в случае, когда в качестве понятия А выступает, например, «горожанин», а в качестве В - «автоводитель».

Подчинение (субординация)

Схематически обозначаются как разные по масштабу круги Эйлера. Отношения между понятиями в данном случае характеризуются тем, что подчиненное понятие (меньшее по объему) полностью входит в состав подчиняющего (большего по объему). При этом подчиненное понятие не исчерпывает полностью подчиняющее.

Например:

А - дерево;

В - сосна.

Понятие В будет являться подчиненным по отношению к понятию А. Так как сосна относится к деревьям, то понятие А становится в данном примере подчиняющим, «поглощающим» объем понятия В.

Соподчинение (координация)

Отношение характеризует два и более понятия, исключающих друг друга, но принадлежащих при этом определенному общему родовому кругу. Например:

А - кларнет;

В - гитара;

С - скрипка;

D - музыкальный инструмент.

Понятия А, В, С не являются пересекающимися по отношению друг к другу, тем не менее, все они относятся к категории музыкальных инструментов (понятие D).

Противоположность (контрарность)

Противоположные отношения между понятиями подразумевают отнесенность данных понятий к одному и тому же роду. При этом одно из понятий обладает определенными свойствами (признаками), в то время как другое их отрицает, замещая противоположными по характеру. Таким образом, мы имеем дело с антонимами. Например:

А - карлик;

В - великан.

Круг Эйлера при противоположных отношениях между понятиями разделяется на три сегмента, первый из которых соответствует понятию А, второй - понятию В, а третий - всем остальным возможным понятиям.

Противоречие (контрадикторность)

В данном случае оба понятия представляют собой виды одного и того же рода. Как и в предыдущем примере, одно из понятий указывает на определенные качества (признаки), в то время как другое их отрицает. Однако, в отличие от отношения противоположности, второе, противоположное понятие, не заменяет отрицаемые свойства другими, альтернативными. Например:

А - сложная задача;

В - несложная задача (не-А).

Выражая объем понятий подобного рода, круг Эйлера разделяется на две части - третьего, промежуточного звена в данном случае не существует. Таким образом, понятия также являются антонимами. При этом одно из них (А) становится положительным (утверждающим какой-либо признак), а второе (В или не-А) - отрицательным (отрицающим соответствующий признак): «белая бумага» - «не белая бумага», «отечественная история» - «зарубежная история» и т. д.

Таким образом, соотношение объемов понятий по отношению друг к другу является ключевой характеристикой, определяющей круги Эйлера.

Отношения между множествами

Также следует различать понятия элементов и множества, объем которых отображают круги Эйлера. Понятие множества заимствовано из математической науки и имеет достаточно широкое значение. Примеры в логике и математике отображают его как некую совокупность объектов. Сами же объекты являются элементами данного множества. «Множество есть многое, мыслимое как единое» (Георг Кантор, основатель теории множеств).

Обозначение множеств осуществляется заглавными буквами: А, В, С, D… и т. д., элементов множеств - строчными: а, b, с, d…и др. Примерами множества могут быть студенты, находящиеся в одной аудитории, книги, стоящие на определенной полке (или, например, все книги в какой-либо определенной библиотеке), страницы в ежедневнике, ягоды на лесной поляне и т. д.

В свою очередь, если определенное множество не содержит ни одного элемента, то его называют пустым и обозначают знаком Ø. Например, множество точек пересечения параллельных прямых, множество решений уравнения х 2 = -5.

Решение задач

Для решения большого количества задач активно используются круги Эйлера. Примеры в логике наглядно демонстрируют связь логических операций с теорией множеств. При этом используются таблицы истинности понятий. Например, круг, обозначенный именем А, представляет собой область истинности. Таким образом, область вне круга будет представлять ложь. Чтобы определить область диаграммы для логической операции, следует заштриховать области, определяющие круг Эйлера, в которых ее значения для элементов А и В будут истинны.

Использование кругов Эйлера нашло широкое практическое применение в разных отраслях. Например, в ситуации с профессиональным выбором. Если субъект озабочен выбором будущей профессии, он может руководствоваться следующими критериями:

W - что я люблю делать?

D - что у меня получается?

P - чем я смогу хорошо зарабатывать?

Изобразим это в виде схемы: круги Эйлера (примеры в логике - отношение пересечения):

Результатом станут те профессии, которые окажутся на пересечении всех трех кругов.

Отдельное место круги Эйлера-Венна занимают в математике (теория множеств) при вычислении комбинаций и свойств. Круги Эйлера множества элементов заключены в изображении прямоугольника, обозначающего универсальное множество (U). Вместо кругов также могут использоваться другие замкнутые фигуры, но суть от этого не меняется. Фигуры пересекаются между собой, согласно условиям задачи (в наиболее общем случае). Также данные фигуры должны быть обозначены соответствующим образом. В качестве элементов рассматриваемых множеств могут выступать точки, расположенные внутри различных сегментов диаграммы. На ее основе можно заштриховать конкретные области, обозначив тем самым вновь образованные множества.

С данными множествами допустимо выполнение основных математических операций: сложение (сумма множеств элементов), вычитание (разность), умножение (произведение). Кроме того, благодаря диаграммам Эйлера-Венна можно проводить операции сравнения множеств по числу входящих в них элементов, не считая их.

Министерство образования, науки и молодежи Республики Крым Малая академия наук «Искатель»

Направление: математика

г. Красноперекопск – 2017

Работу выполнила:

Шумилина Мария Сергеевна,

ученица 7-А класса муниципального бюджетного общеобразовательного учреждения «Средняя общеобразовательная школа № 5» муниципального образования городской округ Красноперекопск

Научный руководитель:

Шеина Елена Николаевна, учитель математики муниципального бюджетного общеобразовательного учреждения «Средняя общеобразовательная школа № 5 » муниципального образования городской округ Красноперекопск

ВВЕДЕНИЕ …………………………………………………………… 3

ГЛАВА 1. Немного из истории…………………………………. 5

ГЛАВА 2. Из теории множеств……………………………………….7

2.1. Понятие множества.……………………………………..8

2.2. Операции над множествами. …………………………..9

ГЛАВА 3. Решение задач с помощью кругов Эйлера ………………..10

ЗАКЛЮЧЕНИЕ…………………………………………………………..22

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ ………………….23

ВВЕДЕНИЕ

Ничто так не способствует

формированию мыслительной культуры,

как решение логических задач. Математика-

не сухая и скучная наука, а полная

необычных и интересных открытий

Решать логические задачи очень увлекательно. Есть люди, для которых решение логической задачи - увлекательная, но несложная задача. Их мозг как луч прожектора сразу освещает все хитроумные построения, и к правильному ответу они приходят необычайно быстро. Замечательно, что при этом не могут объяснить, как пришли к решению.

Логические задачи составляют обширный класс нестандартных задач. Сюда относятся, прежде, всего, текстовые задачи, в которых требуется распознать объекты или расположить их в определенном порядке по имеющимся свойствам.

Существует множество приемов, которые используются при решении текстовых логических задач. Очень часто решение помогает найти рисунок. Использование рисунка делает решение задачи простым и наглядным. Изображение условий задачи в виде кругов Эйлера, как правило, упрощает и облегчает путь к её решению.

Актуальность состоит в том, что задачи имеют практический характер, что немаловажно в современной жизни. Задачи заставляют задумываться, подходить к решению какой-либо проблемы с другой стороны, уметь выбирать из множества способов решения, наиболее простой, легкий путь.

Цель работы:

Познакомится с кругами Эйлера – Венна;

Научиться применять способ решения задач с помощью кругов Эйлера;

Составлять задачи практического содержания.

Глава 1. Немного из истории

Леонард Эйлер, крупнейший математик XVIII в., родился в Швейцарии в 1707г. В 1727 г. по приглашению Петербургской академии наук он приехал в Россию. В Петербурге Эйлер попал в круг выдающихся ученых: математиков, физиков, астрономов, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира. Научное наследие Эйлера поражает своим объемом и разносторонностью. В списке его трудов более 800 названий. Полное собрание сочинений ученого занимает 72 тома. Среди его работ - первые учебники по дифференциальному и интегральному исчислению. В теории чисел Эйлер продолжил деятельность французского математика П. Ферма.

Эйлер много работает в области математического анализа. Ученый впервые разработал общее учение о логарифмической функции. В геометрии Эйлер положил начало совершенно новой области исследований, выросшей впоследствии в самостоятельную науку-топологию.

Имя Эйлера носит формула, связывающая число вершин (В), ребер (Р) и граней (Г) выпуклого многогранника: В -Р + Г = 2. Даже основные результаты научной деятельности Эйлера трудно перечислить. Здесь и геометрия кривых и поверхностей, и первое изложение вариационного исчисления с многочисленными новыми конкретными результатами. У него были труды по гидравлике, кораблестроению, артиллерии, геометрической оптике и даже по теории музыки. Он впервые дает аналитическое изложение механики вместо геометрического изложения Ньютона, строит механику твердого тела, а не только материальной точки или твердой пластины. Одно из самых замечательных достижений Эйлера связано с астрономией и небесной механикой. Он построил точную теорию движения Луны с учетом притяжения не только Земли, но и Солнца. Это пример решения очень трудной задачи.

Последние 17 лет жизни Эйлера были омрачены почти полной потерей зрения. Но он продолжал творить так же интенсивно, как в молодые годы. Только теперь он уже не писал сам, а диктовал ученикам, которые проводили за него наиболее громоздкие вычисления.

С1761 по 1768 год им были написаны знаменитые «Письма к немецкой принцессе», где Эйлер как раз и рассказывал о своем методе, об изображении множеств в виде кругов. Именно поэтому рисунки в виде кругов, обычно называют «кругами Эйлера». Эйлер отмечал, что изображение множеств в виде кругов «очень подходит для того, чтобы облегчить наши рассуждения».

После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781 – 1848). Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шредер (1841 – 1902). Этот метод широко используется в его книге «Алгебра логика». Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843 – 1923). С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера – Венна.

Глава 2. Из теории множеств

2.1. Понятие множества.

Одним из основных понятий, которые используются в математике, является понятие множества. Для него не дается определения. Можно пояснить, что множеством называют произвольную совокупность объектов, а сами объекты – элементами данного множества. Так, можно говорить о множестве учеников в классе (элементы – ученики),множестве дней недели (элементы – дни недели), множестве натуральных делителей числа 6 (элементы – числа 1, 2, 3, 6) и т. д.

В курсах алгебры и алгебры начало анализа чаще всего рассматривают множества, элементами которых являются числа, и поэтому их называют числовыми множествами.

Как правило, множества обозначают прописными буквами латинского алфавита. Например, если множество M состоит из чисел 1; 2; 3, то его обозначают так: M = {1; 2; 3}. Тот факт, что число 2 входит в это множество

(является элементом данного множества M ) записывается с помощью специального значка следующим образом: 2 M ; а то что число 5 не входит в это множество (не является элементом данного множества M ), записывается так: 5 M .

Можно рассматривать также множество, не содержащее ни одного элемента, - пустое множество. Например: множество простых делителей числа 1 – пустое множество.

Для некоторых множеств существуют специальные обозначения. Так, пустое множество обозначается символом , множество всех натуральных чисел – буквой N , множество всех целых чисел – буквой Z , множество всех рациональных чисел – буквой Q , а множество всех действительных чисел буквой R . С помощью кругов Эйлера – Венна это можно изобразить так:

Рис.1

Если каждый элемент множества A является элементом множества B , то говорят, что множество A является подмножеством множества B .

Это записывают следующим образом: A B .

B

A

Рис.2

2.2. Операции над множествами.

Над множествами можно выполнять определенные действия: находить их пересечение, объединение. Дадим определение этих операций и проиллюстрируем их с помощью кругов.

Пересечением множеств A и B называют их общую часть, то есть множество C всех элементов, принадлежащих как множеству A , так и множеству B

Пересечение множеств обозначают знаком ∩ и записывают A ∩ B .

В

Рис.3

Объединением множеств A и B называют множество C , состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств (A или B ). Объединение множеств обозначают знаком
и записывают A
B

Глава3. Решение задач с помощью Кругов Эйлера

Задача № 1.

Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 - и значки, и марки.

Остальные не увлекаются коллекционированием. Сколько школьников не увлекаются коллекционированием.

Решение.

В условии этой задачи не так легко разобраться. Если сложить 23 и 35, то получится больше 52. Это объясняется тем, что некоторых школьников мы здесь учли дважды, а именно тех, которые собирают и значки, и марки.

чтобы легче решать задачу, представим ее данные на следующей схеме

Рис.5

На этой схеме большой круг означает всех школьников, о которых идёт речь. Круг З изображает школьников, собирающих значки (всего их 23), а круг М - школьников, собирающих марки (всего их 35). В пересечении кругов З и М стоит число 16 - это те, кто собирает и значки, и марки. Значит, только значки собирает 23 - 16 = 7 человек, только марки собирает 35 - 16 = 19 человек. Всего марки и значкисобирает19 + 7 + 16 = 42 человека. Остаётся 52 - 42 = 10 человек, не увлечённых коллекционированием. Это число можно вписать в свободное поле круга. Ответ: 10 человек.

Задача 2.

В классе 15 мальчиков. Из них 10 человек занимается волейболом и 9 баскетболом. Сколько мальчиков занимается и тем, и другим?

Решение.

Изобразим условие с помощью кругов Эйлера. Этот рисунок подсказывает нам рассуждения. Разберём это рассуждение и впишем нужное число в каждую из образовавшихся на диаграмме частей.

Пусть всеми видами спорта занимаются х мальчиков. Тогда только волейболом занимаются (10-х) мальчиков, а только баскетболом (9-х) мальчиков. Составим уравнение: 10-х + х+ 9-х=15, откуда х=4

В

10-х Б

х 9-х

Рис.6

Ответ: 4 человека.

Задача № 3.

Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Чучело», 11 человек – фильм «Выше неба», из них 6 смотрели и «Чучело», и «Выше неба». Сколько человек смотрели только фильм «Выше неба»?

Решение: Чертим два множества таким образом: 6 человек, которые смотрели фильмы «Чучело» и «Выше неба», помещаем в пересечение множеств.

15 – 6 = 9 – человек, которые смотрели только «Чучело».
11 – 6 = 5 – человек, которые смотрели только «Выше неба».

Получаем:

Рис.7

Ответ. 5 человек смотрели только «Выше неба».

Задача № 4.

В группе из 80 туристов, приехавших на экскурсию в Москву, 52 хотят посетить Большой театр, 30 - Художественный театр, 12 хотят посетить оба театра, остальные в театры ходить не хотят. Сколько человек не собирается идти в театр?

Решение.

Только большой театр посетят: 52-12=40 туристов;

только художественный театр посетят

30-12=18 туристов;

8
0-(40+18+12)=10 туристов не собираются идти в театр.

Рис.8

Ответ: 10 человек.

Задача № 5.

На полке стояло 26 волшебных книг по заклинаниям. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал Рон?

Решение.

Учитывая условия задачи, чертеж будет таков:

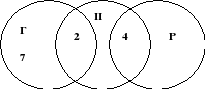
Рис.9

Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри.

Следовательно, 26 – 7 – 2 – 5 – 4 = 8 – книг прочитал Рон. Ответ. 8 книг прочитал Рон.

Задача№6.

В туристической группе из 100 человек 75 человек знают немецкий язык, 65 человек - английский язык, а 10 человек - не знают ни немецкого, ни английского языка. Сколько туристов знают два языка? Решение.

Изобразим условие задачи в виде кругов Эйлера.

Легко видеть, что 90 туристов (100-10) знают хотя бы один язык; Пусть х туристов знают и английский, и немецкий языки. Тогда (65-х) туристов знают только английскй, а (75-х) человек только немецкий. Получим уравнение 65-х+75-х+х=90, откуда х=50 – туристов знают оба языка. Ответ: 50 туристов.

Задача№7.

Сколько человек участвует в прогулке, если известно, что 16 из них взяли бутерброд с ветчиной, 24 - с колбасой, 15 - с сыром, 11 и с ветчиной, и с колбасой, 8 и с ветчиной, и с сыром, 12 и с колбасой, и с сыром, 6-бутерброды всех видов, а 5- взяли пирожки? Решение : Изобразим множества следующим образом: Рис.11

16+24+15-11-8-12+6=30(чел) - участвовали в прогулке и с собой брали бутерброды или 3+2+6+5+7+6+1=30(чел)

30+5=35(чел) - участвовали в прогулке
Ответ. 35 человек

Задача №8

В 5 классе нашей школы 22, в 6 классе – 16, в 7 классе – 23 ребят. Известно, что кружки по лыжам, шахматам и спортивным играм ходят 4 человека. Каждые две секции посещают 9 человек. Сколько человек ходит из каждого класса на секции? Сколько учеников не ходит ни на какой спортивный кружок?

Решение. Если на все три кружка ходят 4 ученика, а на каждые два – 9 человек, то две секции с 5 и 6 класса, с 6 и 7 класса, с 5 и 7 класса посещают по 5

человек.

Рис.12

Получаем 5+5+4=14 пятиклассников посещают кружки, 22-14=8 человек не ходят ни на какой кружков. Рассуждая также, из шестиклассников 16-14=2 ученика никуда не ходя, а из семиклассников – 23-14=9 человек.

Ответ: 14 учеников с каждого класса посещают кружки, не ходят ни на какой из 5-ого – 7, из 6-ого – 2, из 7-ого – 9 учеников.

Задача № 9.

Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?

Решение: В оспользуемся кругами Эйлера.

Рис.13

Всеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят. Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься 8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.
Ответ. 20 человек не умеют кататься ни на одном спортивном снаряде.

Задача № 10 .

В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?

Решение . Д - драмкружок; Х - хор; С - спорт. В круге Д - 27 ребят, в круге Х - 32 человека, в круге С - 22 ученика. Те 10 ребят из драмкружка, которые поют в хоре, окажутся в общей части кругов Д и X. Трое из них ещё и спортсмены, они окажутся в общей части всех трёх кругов. Остальные семеро спортом не увлекаются. Аналогично, 8-3=5

спортсменов, не поющих в хоре и 6-3=3, не посещающих драмкружок. Легко видеть, что 5+3+3=11 спортсменов посещают хор или драмкружок, 22-(5+3+3)=11 заняты только спортом; 70-(11+12+19+7+3+3+5)=10 - не поют в хоре, не занимаются в драмкружке, не увлекаются спортом.

Рис.14 Ответ: 10 человек.

Задача№11 . В классе 30 человек. 20 из них каждый день пользуются метро, 15 - автобусом, 23 - троллейбусом, 10 - и метро, и троллейбусом, 12 - и метро, и автобусом, 9 - и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта?

Решение.

Рис.15

Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом - (10 − х) человек, только автобусом и троллейбусом - (9 − х) человек, только метро и автобусом -(12 − х) человек. Найдем, сколько человек пользуется одним только метро:

20 − (12 − х) − (10 − х) − х = х − 2

Аналогично получаем: х − 6 - только автобусом и х + 4 - только троллейбусом, так как всего 30 человек, составляем уравнение:

х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30.

отсюда х = 3.

Ответ: 3 человека.

Задача № 12.

Из сотрудников фирмы 16 побывали во Франции,10-в Италии,6-в Англии; в Англии и Италии-5; в Англии и Франции -6; во всех трех странах - 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?

Решение:

Нам известно, что во всех трех странах было 5 сотрудников. В Англии и Италии тоже 5, значит эти же сотрудники были и во Франции и поэтому в пересечении кругов А и И ставим 0. В Франции и Италии нам неизвестно поэтому пишем х-5 в пересечении кругов А и Ф. Т.к. в Англии было 6 человек, то 6-5-1=0 пишем 0,во Франции 16-х+5-6 и Италии 10-х+5-5 и всего в фирме 19 сотрудников, то остается составить и решить уравнение: 1+16-х+5-6+5+х-5+10-х+5-5=19, отсюда х=7, значит в Италии и Франции побывало 7-5=2 сотрудника фирмы.

Рис.16

Ответ: 2 сотрудника.

Задача № 13.

Ребят, которые хотят обмениваться различного рода журналами, собралось 10 человек. Среди них выписывают К - 6 человек, Т – 5 человек, Ю – 5 человек, К и Т – 3 человека, Т и Ю -2 человека, К и Ю – 3 человека., а один человек не выписывает ни одного журнала., но читает все эти журналы в библиотеке. Надо узнать, сколько человек выписывают все три журнала, сколько – два, а сколько – только один журнал.

Решение. Пусть большой круг, состоящий из 10 человек, – это множество всех ребят, обменивающихся журналами. Внутри большого круга нарисуем три меньших круга: К, Т, Ю, которые изображают ребят, подписавшихся на соответствующие журналы.. Известно, что один человек не выписывает ни одного журнала.

Пусть х ребят выписывают все три журнала, тогда (3-х)ребят выписывают только К и Т, (2-х) –только Т и Ю, (3-х)- только К и Ю. Значит, только журнал К выписывают 6-(3-х+х+3-х)=х человек, журнал Т 5-(3-х+х+2-х)=х, журнал Ю 5-(3-х+х+2-х)=х.

Рис.17

Составим уравнение: х+3-х+3-х+х+х+х+х+2-х=9, 8+х=9,х=1

Итак, 3 – это число ребят, подписавшихся только на один журнал, 5 – это число ребят, подписавшихся на два журнала, а 1 – число ребят, подписавшихся на все три журнала.

ЗАКЛЮЧЕНИЕ

Предмет математики настолько серьезен,

что нельзя упускать случая сделать

его немного занимательным.

Б. Паскаль

Среди математических задач логические задачи занимают особое место Решение таких задач способствует развитию математического мышления. Они отличаются от большинства математических задач тем, что для их решения часто не требуется запас каких-то специальных знаний, а нужна, как правило, сообразительность. Одна из характерных черт любой логики состоит в том, что она позволяет, получив некоторую информацию, извлечь (выявить) содержащиеся в ней новые знания.

Оказывается приемов, с помощью которых можно решать текстовые логические задачи, несколько. Они разнообразны и каждый из них имеет свою область применения.

В моей работе рассмотрены задачи, которые состоят из множества данных. Найденные решения подчиняются одному и тому же способу: составляем рисунок; заносим первоначальные данные в круги; анализируя и рассуждая, записываем результаты в части кругов; ищем и записываем ответ. Изображение условий задачи в виде кругов Эйлера, как правило, упрощает и облегчает путь к её решению. Кроме того с их помощью можно ответить на множество вопросов, поставленных к одному условию задачи.

Данная тема расширила мой математический кругозор, обогатила арсенал средств, используемых в решении разнообразных задач.

Список используемых источников:

1. Гаврилова Т. Д..Занимательная математика. 5 - 11 классы. Волгоград: Учитель, 2005.-96 с.

2. Германович П.Ю. «Сборник задач по математике на сообразительность».

3. Гетманова А. Д. Логические основы математики 10 – 11 класс: учебное пособие. – М.: Дрофа, 2005.

4. Глейзер Г. И. . - М.: Просвещение, 1964. - С. 232.

5. Гусев В.А., Орлов А.И., Розенталь А.Л. «Внеклассная работа по математике». М.: Просвещение, 1984.

6. Нелин Е.П., Долгова О.Е.. Учебник алгебра и начала анализа 11 класс.

Тезисы к работе

Тема моей исследовательской работы «Решение задач с помощью кругов Эйлера ». При подготовке к олимпиаде я столкнулась с задачами, в которых большое количество данных. Оказывается, упростить решение таких задач помогают так называемые круги Эйлера, с помощью которых можно изобразить множество элементов, обладающих определённым свойством. Целью данной работы является изучение этого способа и умение применять его для решения задач.

В работе рассмотрены задачи, решение которых подчиняются одному алгоритму: составляем рисунок; заносим первоначальные данные в круги, начиная с условия которое содержит больше свойств; анализируя и рассуждая записываем результаты в части круга; записываем ответ.

Актуальность состоит в том, что задачи имеют практический характер, что немаловажно в современной жизни. Задачи заставляют задумываться, подходить к решению какой-либо проблемы с другой стороны, уметь выбирать из множества способов решения, наиболее простой, легкий путь. Способ, рассмотренный в работе доступен и легок в понимании, что позволяет расширить круг его применения. Круги Эйлера можно встретить и в истории, и в биологии, и при изучении других предметов.

Материал,который был исследован в работе,а также практическая часть, могут быть применены на дополнительных занятиях, при подготовке к математическим олимпиадам.

Если вы думаете, что ничего не знаете о кругах Эйлера, вы ошибаетесь. На самом деле вы наверняка не раз с ними сталкивались, просто не знали, как это называется. Где именно? Схемы в виде кругов Эйлера легли в основу многих популярных интернет-мемов (растиражированных в сети изображений на определенную тему).

Давайте вместе разберемся, что же это за круги, почему они так называются и почему ими так удобно пользоваться для решения многих задач.

Происхождение термина

– это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.

Пока не очень понятно, верно? Посмотрите на этот рисунок:

На рисунке представлено множество – все возможные игрушки. Некоторые из игрушек являются конструкторами – они выделены в отдельный овал. Это часть большого множества «игрушки» и одновременно отдельное множество (ведь конструктором может быть и «Лего», и примитивные конструкторы из кубиков для малышей). Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому мы рисуем для них отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.

Ну что, так стало понятнее? Именно поэтому круги Эйлера – это тот метод, который наглядно демонстрирует: лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и проще получить ответ.

Автор метода - ученый Леонард Эйлер (1707-1783). Он так и говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Эйлер считается немецким, швейцарским и даже российским математиком, механиком и физиком. Дело в том, что он много лет проработал в Петербургской академии наук и внес существенный вклад в развитие российской науки.

До него подобным принципом при построении своих умозаключений руководствовался немецкий математик и философ Готфрид Лейбниц.

Метод Эйлера получил заслуженное признание и популярность. И после него немало ученых использовали его в своей работе, а также видоизменяли на свой лад. Например, чешский математик Бернард Больцано использовал тот же метод, но с прямоугольными схемами.

Свою лепту внес также немецкий математике Эрнест Шредер. Но главные заслуги принадлежат англичанину Джону Венну. Он был специалистом в логике и издал книгу «Символическая логика», в которой подробно изложил свой вариант метода (использовал преимущественно изображения пересечений множеств).

Благодаря вкладу Венна метод даже называют диаграммами Венна или еще Эйлера-Венна.

Зачем нужны круги Эйлера?

Круги Эйлера имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, менеджменте и не только.

Если говорить о видах кругов Эйлера, то можно разделить их на те, что описывают объединение каких-то понятий (например, соотношение рода и вида) – мы их рассмотрели на примере в начале статьи.

А также на те, что описывают пересечение множеств по какому-то признаку. Таким принципом руководствовался Джон Венн в своих схемах. И именно он лежит в основе многих популярных в интернете мемов. Вот вам один из примеров таких кругов Эйлера:

Забавно, правда? И главное, все сразу становится понятно. Можно потратить много слов, объясняя свою точку зрения, а можно просто нарисовать простую схему, которая сразу расставит все по местам.

Кстати, если вы не можете определиться, какую профессию выбрать, попробуйте нарисовать схему в виде кругов Эйлера. Возможно, чертеж вроде этого поможет вам определиться с выбором:

Те варианты, которые окажутся на пересечении всех трех кругов, и есть профессия, которая не только сможет вас прокормить, но и будет вам нравиться.

Решение задач с помощью кругов Эйлера

Давайте рассмотрим несколько примеров задач, которые можно решить с помощью кругов Эйлера.

Вот на этом сайте - http://logika.vobrazovanie.ru/index.php?link=kr_e.html Елена Сергеевна Саженина предлагает интересные и несложные задачи, для решения которых потребуется метод Эйлера. Используя логику и математику, разберем одну из них.

Задача про любимые мультфильмы

Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым - «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны».

Решение:

Так как по условиям задачи у нас даны три множества, чертим три круга. А так как по ответам ребят выходит, что множества пересекаются друг с другом, чертеж будет выглядеть так:

Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу:

Выходит, что:

21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».

13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».

Осталось только разобраться, сколько шестиклассников двум другим вариантам предпочитает мультфильм «Губка Боб Квадратные Штаны». От всего количества учеников отнимаем всех тех, кто любит два других мультфильма или выбрал несколько вариантов:

38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».

Теперь смело можем сложить все полученные цифры и выяснить, что:

мультфильм «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек. Это и есть ответ на поставленный в задаче вопрос.

А еще давайте рассмотрим задачу , которая в 2011 году была вынесена на демонстрационный тест ЕГЭ по информатике и ИКТ (источник - http://eileracrugi.narod.ru/index/0-6).

Условия задачи:

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» - символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.

Запрос	Найдено страниц (в тысячах)
Крейсер | Линкор	7000
Крейсер	4800
Линкор	4500

Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор ?

Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.

Опираясь на условия задачи, составим уравнения:

1. Крейсер | Линкор: 1 + 2 + 3 = 7000
2. Крейсер: 1 + 2 = 4800
3. Линкор: 2 + 3 = 4500

Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:

4800 + 3 = 7000, откуда получаем 3 = 2200.

Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:

2 + 2200 = 4500, откуда 2 = 2300.

Ответ: 2300 - количество страниц, найденных по запросу Крейсер & Линкор.

Как видите, круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.

Заключение

Полагаю, нам удалось убедить вас, что круги Эйлера – не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Причем не только абстрактных задач на школьный уроках, но и вполне себе житейских проблем. Выбора будущей профессии, например.

Вам еще наверняка будет любопытно узнать, что в современной массовой культуре круги Эйлера нашли отражение не только в виде мемов, но и в популярных сериалах. Таких, как «Теория большого взрыва» и «4исла».

Используйте это полезный и наглядный метод для решения задач. И обязательно расскажите о нем друзьям и одноклассникам. Для этого под статьей есть специальные кнопки.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Если Вы считаете, что ничего не знаете о таком понятии, как круги Эйлера, то вы глубоко заблуждаетесь. Еще из младшей школы известны схематические изображения, или кружки, позволяющие наглядно осмыслить взаимоотношения между понятиями и элементами системы.

Метод, придуманный Леонардом Эйлером, использовался ученым для решения сложных математических задач. Кругами он изображал множества и сделал эту схему основой такого понятия, как символическая . Метод призван максимально упростить рассуждения, направленные на решении той или иной задачи, именно поэтому методика активно используется как в младшей школе, так и в академической среде. Интересно, что подобный подход был ранее использован немецким философом Лейбницем, а позже был подхвачен и применен в различных модификациях известными умами в области математики. Например, прямоугольные схемы чешского Больцано, Шредера, Венна, известного созданием популярной диаграммы, основанной на этом простом, но удивительно действенном методе.

Круги являются основой так называемых «наглядных интернет мемов», которые основаны на схожести признаков отдельных множеств. Забавно, наглядно, а главное понятно.

Круги мысли

Круги позволяют наглядно описать условия задачи и мгновенно принять верное решение, или выявить направление движение в сторону правильного ответа. Как правило, круги Эйлера используются для решения логико-математических задач, связанных с множествами, их объединениями или частичными наложениями. В пересечение кругов попадают объекты, обладающие свойствами каждого из изображенных кружком множеств. Объекты, не вошедшие в множество, находятся за пределами того или иного круга. Если понятия абсолютно равнозначны, они обозначаются одним кругом, представляющим собой объединение двух множеств, имеющих равные свойства и объемы.

Логика взаимосвязей

Используя круги Эйлера, вы можете решить ряд бытовых задач и даже определиться с выбором будущей профессии, стоит лишь проанализировать свои возможности и желания и выбрать их максимальное пересечение.

Теперь становится ясно, что круги Эйлера вовсе не абстрактное математическое и философское понятие из разряда теоретических знаний, они имеют весьма прикладное и практическое значение, позволяя разобраться не только с простейшими математическими проблемами, но и решить важные жизненные дилеммы наглядным и понятным каждому способом.

Цель урока: Познакомить обучающихся с решением простейших логических задач методом кругов

Задачи урока

• Образовательная : дать обучающимся представление о методе кругов Эйлера;
• Развивающая : развитие логического и аналитического мышления;
• Воспитательная : воспитание умения выслушивать мнение других обучающихся и отстаивать свою точку зрения.

Материал для урока: карточки с заданиями, портрет Л. Эйлера, доска.

Ход урока

1. Организационный момент (3 мин)
2. Разминка (5 мин)
3. Изучение нового материала (5 мин)
4. Первичная отработка метода решения (30 мин)
5. Подведение итогов занятия (2 мин)
6. Организационный момент.

Преподаватель : Здравствуйте, ребята! Сегодня на занятии мы с вами познакомимся с новым для вас методом решения логических задач - кругами Эйлера. Мы научимся решать некоторые из тех зада, которые входят в группу конкурсных и олимпиадных. Целью нашего урока: является познакомиться с решением простейших логических задач методом кругов.

Разминка

Вниманию учащихся предлагается несколько шуточных логических задач, направленных на активизацию мышления обучающихся.

1. Гусь стоит 20 рублей и еще половину того, сколько стоит он на самом деле. Сколько стоил гусь?
2. Два спортсмена на соревновании пробежали по стадиону 8 кругов. Сколько кругов пробежал каждый?
3. Назовите два числа, разность которых равнв их сумме.
4. Сколько будет: два плюс два умножить на два?

Изучение нового материала

Преподаватель: В математике рисунки в виде кругов, изображающих множества, используются очень давно. Одним из первых, кто пользовался этим методом, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646-1716). В его черновых набросках были обнаружены рисунки с такими кругами. Затем этот метод довольно основательно развил и Леонард Эйлер. Он долгие годы работал в Петербургской Академии наук.

Для наглядной геометрической иллюстрации понятий и соотношений между ними используется диаграммы Эйлера-Венна (круги Эйлера). Если имеются какие-либо понятия А, В, С и т.д., то объем каждого понятия (множество) можно представить в виде круга, а отношения между этими объектами (множествами) - в виде пересекающихся кругов.

Перед решением задачи ответьте на следующие вопросы:

1. О скольких множествах идет речь в данной задаче?
2. Какие из перечисленных в задаче данных относятся к разным множествам одновременно?

Первичная отработка метода решения. Обучающимся предлагаются следующие задачи. Первая задача рассматривается подробно. Последующие задачи решаются обучающимися у доски.

Задача 1. Домашние любимцы. У всех моих подруг есть домашние питомцы. Шестеро из них любят и держат кошек, а пятеро - собак. И только у двоих есть и те и другте. Угадайте, сколько у меня подруг?

Решение: Изобразим два круга, так как у нас два вида питомцев. В одном будем фиксировать владелиц кошек, в другом - собак. Поскольку у некоторых подруг есть и те, и другие животные, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кошки и собаки есть у двоих. В оставшейся части "кошачьего" круга ставим цифру 4 (6 - 2 = 4). В свободной части "собачьего" круга ставим цифру 3 (5 - 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.

Ответ. 9 подруг.

Задача 2. Библиотеки. В классе 30 учеников. Все они являются читателями школьной и районной библиотек. Из них 20 ребят берут книги в школьной библиотеке, 15 - в районной. Сколько учеников не являются читателями школьной библиотеки?

Решение: Пусть круг Ш изображает читателей только школьной библиотеки, круг Р - только районной. Тогда ШР - изображение читателей и районной, и школьной библиотек одновременно. Из рисунка следует, что число учеников, не являющихся читателями школьной библиотеки, равно:

(не Ш) = Р - ШР. Всего 30 учеников, Ш = 20 человек, Р = 15 человек. Тогда значение ШР может быть найдено так (см. рисунок): ШР = (Ш + Р) - 30 = (20 + 15) - 30 = = 5, т.е. 5 учеников являются читателями школьной и районной библиотек одновременно. Тогда (не Ш) = = Р - ШР= 15 - 5= 10.

Ответ: 10 учеников не являются читателями школьной библиотеки.

Задача 3. Любимые мультфильмы. Среди школьников пятого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: "Белоснежка и семь гномов", "Винни Пух", "Микки Маус". Всего в классе 28 человек. "Белоснежку и семь гномов" выбрали 16 учеников, среди которых трое назвали еще "Микки Маус", шестеро - "Винни Пух", а один написал все три мультфильма. Мультфильм "Микки Маус" назвали 9 ребят, среди которых пятеро выбрали по два мультфильма. Сколько человек выбрали мультфильм "Винни Пух"?

Решение: В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Только "Белоснежку" выбрали 16-6-3-1=6 человек. Только "Микки-Маус" выбрали 9-3-2-1=3 человека.

Только "Винни-Пух" выбрали 28-(6+3+3+2+6+1)=7 человек. Тогда, учитывая, что некоторые выбрали по несколько мультфильмов, получаем, что "Винни-Пух" выбрали 7+6+1+2=16 человек.

Задача 4. Хобби. Из 24 учеников 5 класса музыкальную школу посещают 10 человек, художественную школу - 8 человек, спортивную школу - 12 человек, музыкальную и художественную школу- 3, художественную и спортивную школу - 2, музыкальную и спортивную школу - 2, все три школы посещает 1 человек. Сколько учеников посещают только одну школу? Сколько учащихся ни в чем себя не развивают?

Решение: В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Только музыкальную школу посещают 10-3-2-1=4 учащихся. Только художественную школу посещают 8-3-2-1=2 учащихся. Только спортивную школу посещают 12-2-2-1=7 учащихся.

Только одну школу посещают 4+2+7=13 учеников.

Ни в чем себя не развивают 24-(4+2+7+3+2+2+1)=3 учащихся.

Ответ. 13 учеников посещают только одну школу, 3 учащихся себя не развивают.

Задача 5. О головоломках. На полке стояло 26 различных математических игр - головоломок. В 4 из них поиграл и Гриша, и Саша. Игорь попробовал проиграть 7 игр, которых не касались ни Гриша, ни Саша, и две головоломки, в которые играл Гриша. Всего Гриша играл в 11 математических игр - головоломок. Во сколько головоломок сыграл Саша?

Решение: Так как Гриша всего проиграл в 11 игр, из них 4 головоломки решены Сашей и 2 головоломки - Игорем, то 11 - 4 - 2 = 5 - игр проиграно только Гришей. Следовательно, 26 - 7 - 2 - 5 - 4 = 8 - головоломок решено только Сашей. А всего Саша играл в игр.

Ответ. 12 игр решил Саша.

Задача 7. Спорт для всех. В классе 38 человек. Из них 16 играют в баскетбол, 17 - в хоккей, 18 - в футбол. Увлекаются двумя видами спорта - баскетболом и хоккеем - четверо, баскетболом и футболом - трое, футболом и хоккеем - пятеро. Трое не увлекаются ни баскетболом, ни хоккеем, ни футболом. Сколько ребят увлекаются одновременно тремя видами спорта? Сколько ребят увлекается лишь одним из этих видов спорта?

Решение. Воспользуемся кругами Эйлера.

Пусть большой круг изображает всех учащихся класса, а три меньших круга Б, Х и Ф изображают соответственно баскетболистов, хоккеистов и футболистов. Тогда фигура Z, общая часть кругов Б, Х и Ф, изображает ребят, увлекающихся тремя видами спорта. Из рассмотрения кругов Эйлера видно, что одним лишь видом спорта - баскетболом занимаются 16 - (4 + z + 3) = 9 - z; одним лишь хоккеем 17 - (4 + z + 5) = 8 - z; одним лишь футболом

18 - (3 + z + 5) = 10 - z. Составляем уравнение, пользуясь тем, что класс разбился на отдельные группы ребят; количества ребят в каждой группе обведены на рисунке рамочкам: 3 + (9 - z) + (8 - z) + (10 - z) + 4 + 3 + 5 + z = 38,z = 2. Таким образом, двое ребят увлекаются всеми тремя видами спорта. Складывая числа 9 - z, 8 - z и 10 - z, где z = 2, найдем количество ребят, увлекающихся лишь одним видом спорта: 21 человек.

Ответ: Двое ребят увлекаются всеми тремя видами спорта человека. Увлекающихся лишь одним видом спорта: 21 человек.

Домашнее задание. Задача 6. Спортивный класс. В классе 35 учеников. 24 из них играют в футбол, 18 - в волейбол, 12 - в баскетбол. 10 учеников одновременно играют в футбол и волейбол, 8 - в футбол и баскетбол, а 5 - в волейбол и баскетбол. Сколько учеников играют и в футбол, и в волейбол, и в баскетбол одновременно?

Подведение итогов занятия

Учащиеся подводят итоги занятия самостоятельно или отвечая на наводящие вопросы:

1. С чем мы познакомились на занятии?
2. В чем заключается этот метод? В чем он заключается?
3. Чему мы сегодня научились на занятии?
4. С чего необходимо начать решение задачи?
5. Какие задачи вызвали у вас наибольшее затруднение? Почему?